Linear regression analysis is generally the choice of researchers to test the effect of one variable on other variables. Various scientific fields, both exact and social sciences, have used this analysis. Maybe you are very familiar with the stages of analysis and how to interpret using this simple linear regression analysis. However, do you understand the chronology of getting the values from the analysis results? It is also important to know and understand well. Based on this background, Kanda Data will discuss manual calculations for simple linear regression analysis on this occasion.
The topic of this discussion is very complex, so this time I will present the discussion in stages. “Why?” Because usually when you talk about math, you need a cup of coffee? 😊. But if you practice gradually and consistently, this calculation method will certainly become easier in the future.
This article will be limited to discussing how to calculate the coefficients bo and b1 manually using Microsoft Excel on simple linear regression. Before discussing further and deeper, you need to know first about simple linear regression. As the name implies, “simple” means not too complex. Simple linear regression is indicated by the number of variables analyzed, which only consist of two variables. So, in a simple linear regression analysis, the tested variable consists of one dependent variable (often denoted by variable Y) and one independent variable (often denoted by variable X).
You need to pay attention to the number of independent variables as only one. “Then what if the number of independent variables is more than one?” So, if the number of independent variables is more than one, for example, two or more independent variables, it is called multiple linear regression. So it’s clear.
Alright, let’s continue our discussion this time. So, calculating the coefficients bo and b1 manually can use two ways. You can directly calculate using a formula based on the initial observation value (variable values of Y and X) or by using a formula that needs first to calculate the difference in the value of each observation with the average value.
Calculation of coefficients bo and b1 (1st way)
Before starting to do the calculations, you can grab a cup of coffee and a snack because we’re going to discuss the steps that are a little more serious 😊. I will continue, so in calculating the coefficients of bo and b1, this means that you will calculate the estimated coefficient value of the intercept variable (bo) and the estimated coefficient of the variable X (b1). In the econometrics book written by Koutsoyiannis (1977), to distinguish the estimate from the sample, you can add a hat mark above bo and b1.
“Where’s the calculation formula?” ok, so the formula for calculating the coefficients bo and b1 for this 1st method refers to book written by Koutsoyiannis (1977), namely:
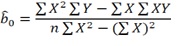
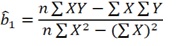
Based on this formula, you need to know that the sigma sign indicates the total sum, and “n” means the number of observations/number of data/number of samples analyzed. As for “Y” is the initial value of the observation variable Y, and for “X” it is the initial value of the observation variable X. Then “XY” is the multiplication between the observations of variable X and variable Y. At the same time, if there is a square sign, you need to square all data before summing.
Until this stage, do you feel dizzy? If yes, that’s reasonable 😊. Alright, if you are still confused, maybe you will be more helpful if a calculation method is packaged in audio-visual form. It just so happens that I already have a video tutorial on how to calculate the 1st method as below (video in Indonesian, please use subtitles):
Hopefully, you are not confused anymore after watching the video tutorial. If you still have questions, you can comment on this article or in the comments column of your watched video. OK, let’s move on to the second calculation method.
Calculation of coefficients bo and b1 (2nd way)
The method of calculating the coefficients of bo and b1 using the second method is simpler in the formula when compared to the first method. In some books, it is often denoted by y (small) and x (small). But suppose you want to choose to calculate the coefficients using this 2nd method. In that case, you need first to calculate the difference between each observation value of variable Y and variable X with the average value. Referring to the book written by Koutsoyiannis (1977), the calculation formula for the second method is:
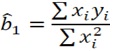

Through this 2nd method, you need to calculate the b1 coefficient value first before calculating the bo coefficient value. This method is because one of the components of calculating the bo value must be a b1 coefficient. Thus you need to count them in order! As in the calculation of the 1st method, I have also prepared a video tutorial as in the following video (video in Indonesian, please use subtitles):
Alright, up to this point, you seem to have been thinking seriously. 😊 Come on, it’s time to relax for a moment while recapping the topic this time. In this article, our topic is the calculation of the coefficients of bo and b1 in simple linear regression using excel as described in the complete video tutorial. In manual calculations on this simple linear regression, there are two ways: directly calculating using the original sample observation and deviations of the variables from their means.
Keep up the good work, and stay healthy! Don’t be tired to keep learning and sharing useful things! Wait for the next article update!


[…] The coefficient of determination in regression analysis has an important function. Therefore, it is not surprising that various research papers using regression analysis will generally always bring up the value of the coefficient of determination. Based on this, Kanda data will write this topic to be discussed together. This article continues the previous week’s theme, which discussed manually calculating the coefficients bo and b1 in simple linear regression. […]